Prove That There Exists Continuous Increasing Function G and G F is Integrable
MATH 554 - INTEGRATION
Handout #9 - 11/20/97
Defn . A collection of n+1 distinct points of the interval [a,b]
is called a partition of the interval. In this case, we define the norm of the partition by
where 
is the length of the i-th subinterval 
.
Defn . For a given partition P, we define the Riemann upper sum of a function f by
where 
denotes the supremum of f over each of the subintervals . Similarly, we define the Riemann lower sum of a function f by
where 
denotes the infimum of f over each of the subintervals . Since 
, we note that
for any partition P.
Defn . Suppose 
are both partitions of [a,b], then 
is called a refinement of 
, denoted by
if as sets 
.
Note . If
, it follows that 
since each of the subintervals formed by is contained in a subinterval which arises from .
Lemma . If , then
and
Proof. Suppose first that is a partition of [a,b] and that is the partition obtained from by adding an additional point z. The general case follows by induction, adding one point at at time. In particular, we let
and
for some fixed i. We focus on the upper Riemann sum for these two partitions, noting that the inequality for the lower sums follows similarly. Observe that
and
where 
and 
. It then follows that 
since
Defn . If and are arbitrary partitions of [a,b], then the common refinement of and is the formal union of the two.
Corollary . Suppose and are arbitrary partitions of [a,b], then
Proof. Let P be the common refinement of and , then
Defn . The lower Riemann integral of f over [a,b] is defined to be
Similarly, the upper Riemann integral of f over [a,b] is defined to be
By the definitions of least upper bound and greatest lower bound, it is evident that for any function f there holds
Defn . A function f is Riemann integrable over [a,b] if the upper and lower Riemann integrals coincide. We denote this common value by 
.
Examples :
Theorem . A necessary and sufficient condition for f to be Riemann integrable is given 
, there exists a partition P of [a,b] such that
Proof. First we show that (*) is a sufficient condition. This follows immediately, since for each that there is a partition P such that (*) holds,
Since was arbitrary, then the upper and lower Riemann integrals of f must coincide.
To prove that (*) is a necessary condition for f to be Riemann integrable, we let 
By the definition of the upper Riemann integral as a infimum of upper sums, we can find a partition of [a,b] such that
Similarly, we have
Let P be a common refinement of and , then subtracting the two previous inequalities implies,
Defn . A Riemann sum for f for a partition P of an interval [a,b] is defined by
where the 
, satisfying 
), are arbitrary.
Corollary . Suppose that f is Riemann integrable on [a,b], then there is a unique number 
(
such that for every there exists a partition P of [a,b] such that if 
, then
where 
is any Riemann sum of f for the partition . In this sense, we can interpret
although we would actually need to show a little more to be entirely correct.
Proof. Since 
for all partitions, we see that parts i.) and ii.) follow from the definition of the Riemann integral. To see part iii.), we observe that 
and hence that
But we also know that both
and condition (*) hold, from which part iii.) follows. 
Theorem . If f is continuous on [a,b], then f is Riemann-integrable on [a,b].
Proof. We use the condition (*) to prove that f is Riemann-integrable. If , we set 
. Since f is continuous on [a,b], f is uniformly continuous. Hence there is a 
such that 
if 
. Suppose that 
, then it follows that 
. Hence
Theorem . If f is monotone on [a,b], then f is Riemann-integrable on [a,b].
Proof. If f is constant, then we are done. We prove the case for f monotone increasing. The case for monotone decreasing is similiar. We again use the condition (*) to prove that f is Riemann-integrable. If , we set 
and consider any partition P with . Since f is monotone increasing on [a,b], then 
and 
. Hence
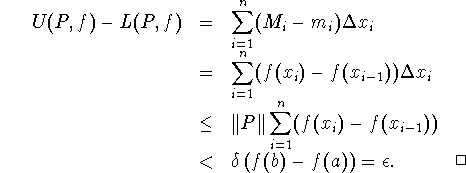
Theorem . (Properties of the Riemann Integral) Suppose that f and g are Riemann integrable and k is a real number, then
- i.)
- ii.)
- iii.)
implies 
. - iv.)
Proof. To prove part i.), we observe that in case 
, then 
and 
. Hence U(P,kf)=kU(P,f) and L(P,kf)=kL(P,f). In the case that k;SPMlt;0, then 
and 
. It follows in this case that U(P,kf)=kL(P,f) and L(P,kf)=kU(P,f) and so
To prove property ii.) we notice that 
and 
for any interval I (for example, 
). Hence,
Let , then since f and g are Riemann integrable, there exist partitions such that
If we let P be a common refinement of and , then by combining inequalities (1) and (2), we see that see that
Property iii.) follows directly from the definition of the upper and lower integrals using, for example, the inequality 
.
Property iv.) is proved by applying property iii.) to the inequality
from which it follows that 
. But this inequality implies property iv.).
Defn . We extend the definition of the integral to include general limits of integration which are consistent with our earlier definition.
-
. -
.
Theorem . If f is Riemann integrable on [a,b], then it is Riemann integrable on each subinterval 
. Moreover, if 
, then
Proof. We show first that condition (*) holds for the interval [c,d]. Suppose , then by (*) applied to f over the interval [a,b], we have that there exists a partition P of [a,b] such that condition (*) holds. Let 
be the refinement obtained from P which contains the points c and d. Let 
be the partition obtained by restricting the partition to the interval [c,d], then
and so f is Riemann integrable over [c,d].
To prove the identity (3), we use the fact that condition (*) holds when f is Riemann integrable. Let , then for 
, we may apply (*) to each of the intervals I=[a,b], [a,c] and [c,b], respectively, to obtain partitions 
which satisfy
We let P be the partition of [a,b] formed by the union of the two partitions 
, and be the common refinement of P and 
. Observing that
we can combine with inequality (4) to obtain
Since was arbitrary, then equality (3) must hold.
Theorem . (Intermediate Value Theorem for Integrals) If f is continuous on [a,b], then there exists 
between a and b such that
Proof. Since f is continuous on [a,b] and for 
there holds
then by the Intermediate Value Theorem for continuous functions, there exists a 
such that 
.
Theorem . (Fundamental Theorem of Calculus, Part I. Derivative of an Integral) Suppose that f is continuous on [a,b] and set 
, then F is differentiable and F'(x) = f(x) for a<x<b.
Proof. Notice that
for some between 
and 
. Hence, as 
, then 
converges to and so the displayed difference quotient has a limit of 
as .
Theorem . (Fundamental Theorem of Calculus, Part II. Integral of a Derivative) Suppose that F is function with a continuous derivative on [a,b], then
.
Proof. Define 
, and set H:=F-G. Since the derivative of H is identically zero by Part I of the Fundamental Theorem of Calculus, then the Mean Value Theorem implies that H(b) = H(a). Expressing this in terms of F and G gives
which establishes the theorem.
Robert Sharpley
Fri Jan 9 23:07:34 EST 1998
Source: https://people.math.sc.edu/sharpley/math554_s96/554_9/
0 Response to "Prove That There Exists Continuous Increasing Function G and G F is Integrable"
Post a Comment